Working with pointers
Table of contents
Grasping
V1V2P1P2
In the exercise v1v2p1p2, we will ask you to execute and the following snippet and return the result.
int v1 = 10;
int v2 = 25;
int *p1 = &v1;
int *p2 = &v2;
*p1 += *p2;
p2 = p1;
*p2 = *p1 + *p2;
cout<< v1 << " " << v2 << endl;
cout<< *p1 <<" " << *p2 << endl;
parameterMystery1
We repeat the same concept in ParameterMystery1, and ask you to give the result of the program:
int parameterMystery1(int a, int &b, int* c)
{
b++;
a += *c;
cout<< b << " "<< *c<< " " << a << " " << c << endl;
c = &a;
return a-b;
}
int main()
{
int a = 4;
int b = 8;
int c = -3;
int d;
d = parameterMystery1(a, b, &c);
parameterMystery1(c, d, &b);
parameterMystery1(b, a, &d);
cout<< a <<" " << b << " " << c <<" " <<d << endl;
}
In order to get a constant result, we will suppose that following memory placements.
- a is stored in
0xaa00 - b is stored in
0xbb00 - c is stored in
0xcc00 - d is stored in
0xdd00
parameterMystery2X
Here is another one in ParamterMyster2,
string * parameterMyster2X(string & s1, string s2)
{
s1 += "1";
s2 += "2";
cout<< s2 << " -- " << s1 <<endl;
s1 += "!!!";
return &s1;
}
int main()
{
string s1 = "hi";
string s2 = "bye";
string s3 = "yo";
string * s4 = new string(s3);
string* s5 = nullptr;
parameterMyster2X(s1, s3);
s5 = parameterMyster2X(*s4, s2);
parameterMyster2X(s2, *s5);
cout<<s1<<" "<<s2<<" "<<s3<<endl;
cout<<s4<< " " << *s4 << " " << s5 << *s5 << endl;
}
Les espaces mémoires des variables est le suivant:
- s1 is stored in
0x1100 - s2 is stored in
0x2200 - s3 is stored in
0x3300 - s4 is stored in
0x4400 - s5 is stored in
0x5500
Arrays using pointers
Now is the time to test your understanding of pointers and arrays to solve
some difficult problems. We will provide you with a cmake project which needs
the library google test.
In case you cannot install this library, replace the test with your proper
assert.
Download the attached project in Pointer_homework.zip
Pivot Index
Given an arrays nums, compute its pivot index.
The pivot index of an array is an index where the sum of the elements on its strict left is equal to those on the strict right.
- For the index \(8\), the sum to the left is considered to be \(0\).
- Same goes for the end of the array.
Write a function with the following prototype:
int pivotIndex( vector<int> & nums)
{
}
The function must return the index of the first occurrence of a pivot index otherwise \(-1\).
Example 1
Input: nums = [1,7,3,6,5,6]
Output: 3
Explanation:
The value of the pivot is 3.
Left sum= nums[0] + nums[1] + nums[2] = 1 + 7 + 3 = 11
Right sum = nums[4] + nums[5] = 5 + 6 = 11
Example 2
Input: nums = [1,2,3]
Output: -1
Explanation:
There is no pivot index.
Example 3
Input: nums = [2,1,-1]
Output: 0
Explanation
The pivot index is 0.
Left sum = 0 (no elements)
Right sum = nums[1] + nums[2] = 1 + -1 = 0
The test file for this function is in the file array_pivot.cpp.
Largest Number
Given an integer vectors nums, find if the largest element is as large as
twice the other elements.
In case this element doesn’t exists, return -1;
The real challenge is implement this function using pointers and only one pass of the array.
Example 1
Input: nums = [3, 6, 1, 0]
Output: 1
Explanation: 6 is the largest element, and for each element in the array 6 >=
2*x
Example 2
Input: nums = [1, 2, 3, 4]
Output: -1
Explanation: there is no large element, since 4 <= 2 *3
The starting code of this function is in largest_number.cpp.
Plus One
Given an non empty STL vector representing a number \(n\), write a function that return the vector representation of \(n+1\).
Here is the prototype of the function:
vector<int> plusOne(vector<int> & nums)
{
}
Example 1:
Input: digits = [1,2,3]
Output: [1,2,4]
Example 2:
Input: digits = [4,3,2,1]
Output: [4,3,2,2]
Example 3:
Input: digits = [0]
Output: [1]
The implementation is in add_one.cpp.
Matrices
Pascal Matrix
Write a function generate(int numRows) that gets an integer representing the
number of rows numRows and return a matrix storing the pascal triangle.
In this triangle, each element is computed by using the previous row, as shown in the following figure:
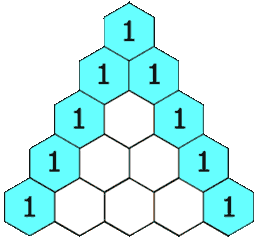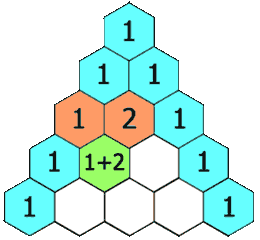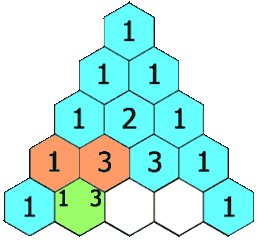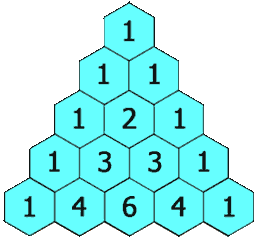
You have the choice to represent this matrix either by using an STL vector or a dynamic memory allocation.
Example 1
Input: numRows = 5
Output: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]
Example 2:
Input: numRows = 3
Output: [[1],[1,1],[1,2,1]]
The starting code is in pascal_matrix.cpp.
Spiral
Given a matrix of size m x n, write a function that return the sprial
traversal of this matrix.
vector<int> spiralOrder(vector<vector<int>> & M)
Example 1
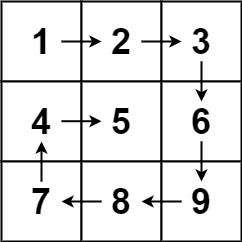
Input: matrix = [[1,2,3],[4,5,6],[7,8,9]]
Output: [1,2,3,6,9,8,7,4,5]
Example 2
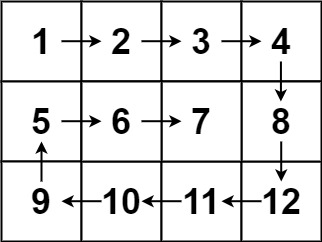
Input: matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
Output: [1,2,3,4,8,12,11,10,9,5,6,7]
