Sorting

Contents

1. Introduction
2. Bubble Sort
   • Bubble
   • Invariant and complexity
   • repeated Bubble
3. Selection Sort
   • Selection
   • Invariant and complexity
4. Insertion Sort
   • insertion
   • Invariant and Complexity
5. Merge Sort
   • Merging
   • Complexity

Introduction

L’opération de tri (Sorting) consiste réarranger les éléments d’un tableau selon un ordre donné.

Input : Une séquence (array) de nombres \((a_1, a_2, \ldots , a_n)\) Output: Une permutation (rearangement) \((a_1^{'}, a_2^{'}, \ldots, a_n^{'})\) tel que

Souvent on se réfère aux valeurs de ce tableau par Keys(clés).

Bubble sort

Le premier algorithme classique est le Tri a bulles. Son concept est de faire monter une plus grande valeur ( comme une bulle) à la surface.

Cette opération est réalisée en permutant deux clés consécutives s’ils sont mal ordonnés.

Animation du tri a bulles.

Bubble

L’opération de base de ce tri, est la montée de bulle. Cette opération consiste a comparer deux clés successives et de les permuter en cas ou elles sont mal ordonnes. Voici un fonction qui réalise cette opération entre deux emplacement mémoire qui dénotent le début et fin d’un tableau.

void bubble( int * begin, int *end)
{
    /* execute a bubble operation from begin to end (non incluse)
     * begin : pointer on the first memory address
     * end   : pointer on the last memory address
     */

    // initiating a pointer on the first value
    auto curr = begin;

    while( curr < end - 1)
    {
        if ( *curr > *(curr + 1) )
            swap(*curr, *(curr + 1));
        
        curr++;
    }
}

Invariant and complexity

Dans l’analyse des algorithmes de tri, on s’intéresse souvent a la propriétés invariant de boucle qui résume le principe que l’algorithme de tri essaie de conserver a fin de réaliser le tri. Par exemple pour le tri a bulles ou essaie a chaque itération de mettre la plus grande valeur a sa place. On aura que:

Invariant:

Après k itérations de bubble, les \(k\) plus grandes valeurs seront a leurs places.

Corollaire:

Après \(\;n-1\) itérations de bubble, le tableau sera trié.

repeated Bubble

Ainsi selon la propriété invariant de boucle, le tableau sera trie si on réalise \(n-1\) opérations de bubble.

void bubble_sort(int * begin, int * end)
{
    // function to perform a bubble sort in the array
    // delimited by begin and end
    while(end > begin)
    {
        bubble(begin, end);
        end --;
    }
}

Pour l’étude de complexité, soit \(T(n)\) le nombre d’opérations qu’on doit effectuer pour trier un tableau de taille \(n\). Pour ce faire, on doit lancer \(n-1\) opérations de bubble ( la taille de tableau est réduite dans chaque itération).

Où \(B(n)\) est le nombre d’opération de la fonction bubble. Or on sait que \(B(n) = n\). Ainsi on obtient que:

Selection Sort

Le tri de Sélection Selection sort un tri qui consiste, a chaque itération, d’identifier l’indice de la plus petite valeur et la permuter avec celle qui occupe sa place (indice 0).

On doit répéter ce mécanisme jusqu’à ce que toutes les valeurs occupent leurs places pour le tri. Un illustration de ce mécanisme est présentée dans la figure suivante:

Illustration du mécanisme de tri par sélection. Les valeurs jaunes sont déjà tries. Les valeurs rouges indiquent l'emplacement de valeur minimal et les valeurs bleues sont celle considères dans la boucle.

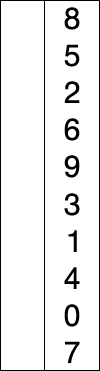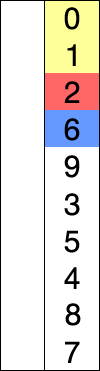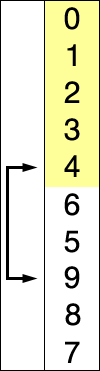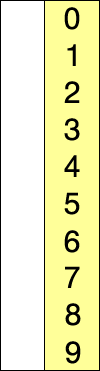
Selection

Afin d’implémenter ce tri, nous commençons par l’opération de base Selection qui doit trouver l’indice de l’élément minimal et permuter ce dernier avec la première valeur.

void selection(int * begin, int * end)
{
    /* Perform a single selection step between 
     * the start memroy [begin] and the end [end]
     */
    auto curr = begin;     // current pointer ( blue in animation)
    auto min  = begin;     // minimal value   ( Red in animation)

    while (curr < end) {
      // update relation
      if (*curr < *min)
        min = curr;

      curr++;
    }

    //Swap if necessary
    if ( min != begin)
        swap(*min, *begin);
}

Finalement pour trier tous les elements, on doit repeter cette operation \(n - 1\).

void selection_sort( int * begin, int *end)
{
    // Performs a selection sort between begin and end 
    //
    while ( begin < end)
    {
        selection(begin, end);
        begin ++;
    }
}

Invariant and complexity

Similaire au tri à bulles, on doit presenter l’invariant de boucle pour le tri de selection. Selon la construction on peut voir clairement que:

Invariant de boucle:

Apres \(k\) selections, on est sur que les \(k\) premières clés sont triés et aussi ils sont à leurs places!

Corollaire:

Apres \(n-1\) iterations de selectins, le tableau sera trié.

• Afin de mieux comprendre cette notion d’invariant de boucle, Essayer de resoudre l’exercice suivant Selection Sort Mystery

Pour l’analyse de complexite, on evalue tout d’abord la complexite d’une operation de selection sur un tableau de taille \(N\). On note ainsi \(S(N)\) pour completer cette operation.

Pour calculer la cle la plus petite, on doit parcourir tout le tableau. Puis on doit realiser une operation de permuation. Ainsi on a

Finalement pour la complexite de tout le tri de selection, on repete \(n-1\) qui sont de taille \(n\) puis \(n-1\) jusqu’a \(2\).

Insertion Sort

Le tri d’Insertion est le tri qu’on réalise naturellement comme humains. Pensez a votre jeu de carte. Comment vous faites pour orgraniser et trier votre main.

insertion

Pour ce tri, l’opération de base et celle d’Insertion qui suppose qu’on dispose d’un tableau deja trié et on cherche à inserer une nouvelle valeur tout en gardent la propriété de tri.

Dans l’image suivante on explique cette operation pour un tableau simple de taille \(6\).

Illustration du processus de tri par insertion. Les valeurs en gris montre le tableau trié (main). La valeur en noir est la valeur a insérer.

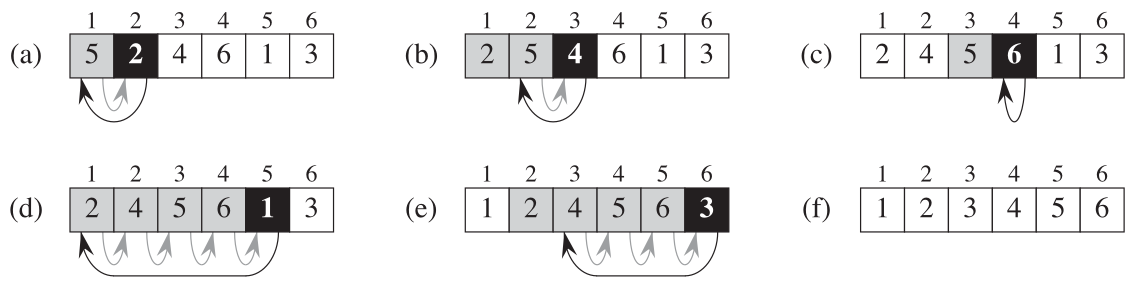
Ainis la premiere fonction a coder est:

void insertion( int * begin, int *end , int value)
{
  // insert the value [value] in the array
  // stored between [begin] and [end]

  auto curr = end;

  // search place for value
  while (curr > begin && *(curr-1) > value) {
    // save next place
    *curr = *(curr-1);

    curr--;
  }
  *curr = value;
}

Le tri par insetion répète cette insertion sur chaque nouvelle valeur du tableau comme illustrée dans la figure suivante:

Animation du tri d'insertion.

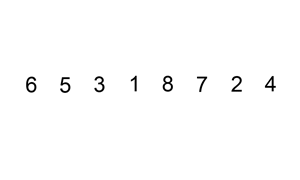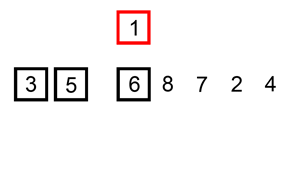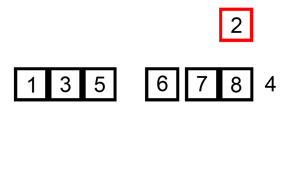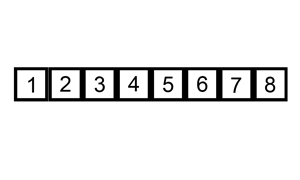
vod insertion_sort(int *begin, int *end)
{
    auto curr = begin + 1;

    while( curr < end)
    {
        insertion(begin, curr, *curr);
        curr ++;

    }
}

Invariant and Complexity

Comme le montre la figure après chaque itération de ce tri, on possède un main ( tableau) qui est trie. Cependant est ce que chaque carte est a sa place finale? La réponse est Non.

Invariant:

Après \(k\) insertions , les \(k\) premiers éléments du tableau sont triés.

Corollaire:

Après \(\;n-1\) itérations d’insertions, le tableau sera trie.

Voici un exercice pour tester cette propriété d’invariance pour ce tri. Insertion Mysteyry

Même si ce tri propose des améliorations par rapport aux tris précédents, il garde une complexité quadratique.

Merge Sort

Le tri par fusion merge sort est votre premier algorithme de tri avance qui utilise les paradigme de divide and conquer. Ce paradigme utilise la récursivité afin de décomposer le problème de tri en sous problèmes (divide) puis regroupe la solution de ces problèmes (conquer).

• Le principe de tri consiste a chaque itération de décomposer le tableau en deux.

• On tri chaque sous tableau séparément.
• Puis on fusionne les deux tableaux triés.

Le concept de ce tri est illustre dans la figure suivante:

Illustration du processus de tri par fusion. Le principe consiste a décomposer à chaque fois le tableau en deux puis trier chaque tableau à part. Une fois on termine, on fusionne les deux parties tout en gardant le tri.

Merging

Pour implémenter ce tri, on doit tout d’abord commencer par l’opération de base qui fusionne deux tableau tries en un seul tableau tout en gardant le tri. Cette opération est illustrée dans la figure suivante:

Principe de fusionner deux tableaux en un seul tableau trié.

Remarquer que la fusion est réalisée dans un autre espace mémoire additionnel.

vecI merge(vecI & L, vecI & R)
{
    // function to merge two sorted arrays [L] and [R]
    
    // result vector
    vecI M(L.size() + R.size());

    int i = 0;            //indice i de Left
    int j = 0;            //indice j de Right
    int k = 0;            // indice de fusion

    // boucle deux elements existents
    while( i < L.size() && j < R.size())
    {
        //comparaison pour verifier la petite valeur
        if ( L[i] < R[j])
            M[k++] = L[i++];
        else
            M[k++] = R[j++];
    }

    //terminer les tableaux
    while(i < L.size())
        M[k++] = L[i++];

    while( j < R.size())
        M[k++] = R[j++];

    return M;
}

Une animation de ce tri en action est présentée dans la figure suivante:

Animation de tri par fusion.

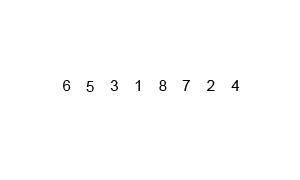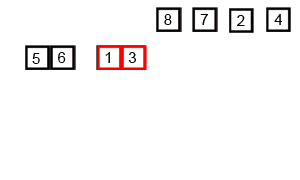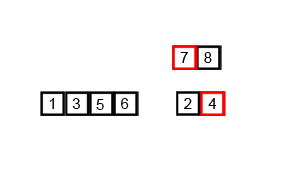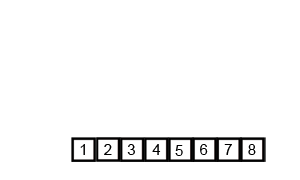
Complexity

Pour l’analyse de complexité, on doit calculer les Coefficients de la formule de récurrence.

• Chaque problème est décompose en deux sous problèmes. \(a = 2\).
• La taille de chaque sous problème est \(\dfrac{n}{2}\) donc \(b = 2\).
• Finalement le coût de décomposition est l’algorithme de fusion, qui est linéaire. Ainsi on a \(d = 1\).

Aini on obtient que:

Si on applique le théorème de master on trouve que:

Deja ca constitut une amelioration importante comparee aux trois tries precedents.