1. Towers of Hanoi
  2. What is Recursion
  3. Basic Examples
  4. Memoization
  5. Complexity Analysis
  6. Tower Hanoi code

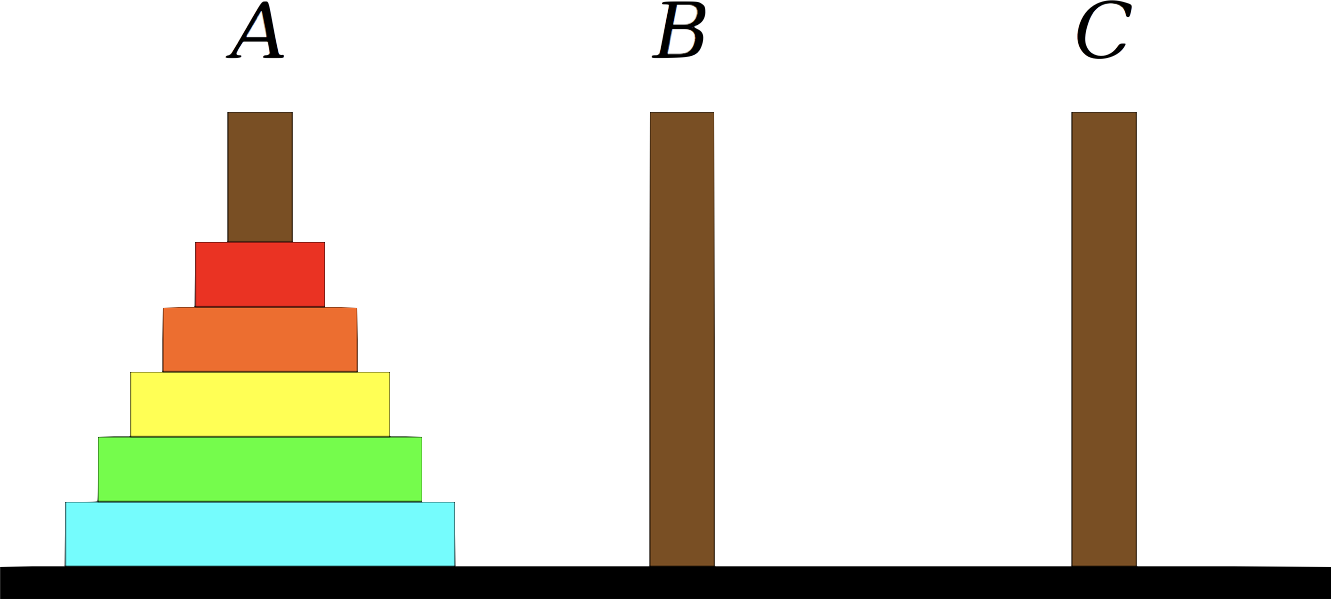
Towers of Hanoi

Le problème de Tour de Hanoi est un problème classique qui demande a l’utilisateur de déplacer un ensemble de disques entre des tiges selon les règles suivantes:

Modèles de tour de Hanoi avec 8 disques.
  1. L’objectif est de déplacer tous les disques d’une tige initiale a une autre.
  2. On ne peut déplacer qu’un disque a la fois.
  3. On ne peut déplacer un disque sur un autre plus grand.

Peut on résoudre ce problème? Si oui comment?

  • Il s’avère qu’il existe une solution mathématique a ce problème.
  • La preuve donne exactement la méthode pour résoudre ce problème.

En cas, ou vous n’êtes pas convaincu, voici une demo qui montre la solution.

Vidéo illustrant la solution du problème de tour de Hanoi pour 5 disques.

Comment peut on résoudre ce problème avec les processus classiques.

A ce stade, on connait qu’une solution récursive a ce problème!!. Si vous n’êtes pas convaincu, essayez de fournir une solution itérative!!!

A la fin, de cette lecture, vous pouvez proposer une solution simple et élégante a ce problème.

What is Recursion

La récurrence est une technique pour résoudre un problème en le réduisant a des simples de problèmes de la même nature.

On peut se demander, comment peut on résoudre un probleme en invoquant le même problème. L’astuce consiste a reduire la complexité en chaque appel. Cette réduction continue jusqu’à atteindre un cas simple ou on connait la réponse. Ce cas est appel base case.

Why Recursion

La récursivité offre:

  1. Une solution élégante est simple.
  2. Outil très puissant de résolution de problème.
  3. Maitriser le flux d’exécution.

On rencontre plusieurs exemples récursives dans la vie réelle, A titre d’exemple, on mentionne le jigsaw puzzle:

Comment peut on résoudre ce problème?
  • Seule procédure possible est celle récursive.
  • Trouver un morceau correcte, placer le.
  • Continuez avec un problème moins simple (contient mois de pièce).

Afin d’illustrer ces concepts, nous allons illustrer ce par un exemple

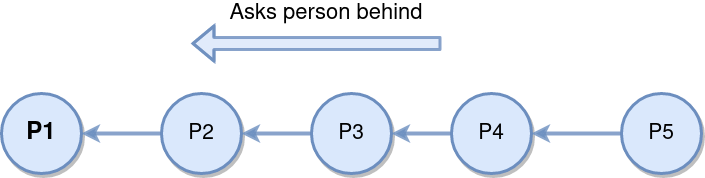
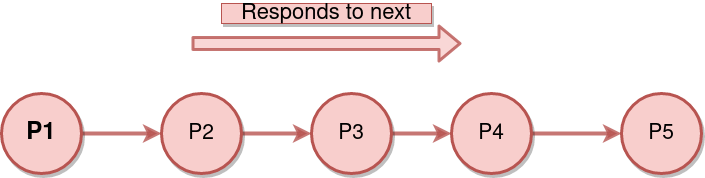
Counting People

On considere le probleme de calculer le nombre de personnes dans une file.

On veut compter le nombre de personne dans cette file. Le problème est que chaque personne ne peut parler qu’a ceux dans son voisinage. Plus précisément, on fixe les deux règles suivantes:

  1. Une personne peut regarder devant et derrière lui.
  2. Une personne peut demander des questions aux personnes devant ou derrière.

Comment peut on résoudre ce problème?

  • Solution: Récurrence
  1. Chaque personne récupère la réponse de celle derrière lui et la reporte a celle devant lui.
int countPersons( Person P)
{
    if(noOneBehind(p))
        return 1;
    else
    {
        auto behind = countPersons(P.getBehind());
        
        return behind + 1;
    }
}

The Three Must

Concevoir un programme ou fonction récursive nécessite:

  • Cas de base: Le cas simple ou on peut facilement répondre a la question.

Par exemple, dans le cas de calcul du nombre de personnes, la personne a la fin connait qu’il y as personne derrière lui.

  • Relation de récurrence: Plus complique a générer, elle consiste le cœur de la réduction du problème. Elle décrit le problème en terme de problèmes de même type mais moins complique.

Dans exemple de calcul des personne, la relation de récurrence indique simplement que le nombre de personnes sera \(1\) plus le nombre de personne derrière moi.

Ainsi pour concevoir une fonction récursive, il faut assurer que votre code:

  1. Votre Code doit une cas pour tous les arguments.
  2. Vous devez avoir un cas de base.
  3. Votre relation de récurrence doit générer un appel plus simple.

Pour le reste, vous devez avoir un foi que votre code va donner le bon resulat :)

The leap of faith.

Basic Examples

Cette section introduit des exemples classiques pour apprendre le paradigme de récurrence. C’est votre entrée principale pour se familiariser avec tous les concepts de ce paradigme:

Factorial

Considérons comme premier exemple, le calcul du factoriel d’un entier naturel \(n\).

\[n! = n \times (n-1) \times (n-2) \ldots 3 \times 2 \times 1\]

On connait déjà comment implémenter une fonction iterative de cette fonction, cependant dans cet exercice, on veut concevoir une fonction recursive.

On va proposer deux versions erronés afin que vous puisez identifier les points manquants soulevées dans la section précédente.

int fact(int n)
{
    //base case
    if ( n == 1)
        return 1;
    else
        return n * n-1 * fact(n-2);
}

Télécharger le projet factorial.zip et ajouter cette implémentation pour voir le résultat.

Une deuxieme version, qui est aussi erronee est:

int main( int n)
{
    // Base case
    if ( n== 0 || n == 1 )
        return 1;

    // Recurrence
    else
        return fact(n+1) / n;
}

Quel est le problème de cette implémentation?

Finalement la version correcte est:

int main( int n)
{
    // Base case
    if ( n== 0 || n == 1 )
        return 1;

    // Recurrence
    else
        return n * fact(n-1);
}

Une question qu’on doit aussi mentionner, est comment calculer la complexité de cette fonction avec cet appel récursif?

Power of X

Un autre exemple classique de récursivité est le calcul de la puissance d’un nombre \(x\) a la puissance \(n\).

float power(float x, int n)
{
    //fonction recursive pour cacluler x^n
}

Avant de lire la suite, essayer de proposer une implémentation vous même, en répondant aux questions suivantes.

Voici le code de projet power.zip avec des simples tests.

  1. Quel est le cas de base?
  2. Quelle est la relation de recurrence?
  3. Quelle est la complexité de votre implémentation?

Première tentative

On va se baser sur la relation suivante:

\[x^n = \left\{ \begin{array}{ll} 1 & \text{si} & n=1\\[2pt] x \times x^{n-1} & \text{sinon} \end{array}\right.\] 
float power(float x, int n)
{
    //base case
    if ( n == 0)
        return 1;
    
    //recurrence relation
    return x * power(x, n-1);
}

Si on analyse de la complexité de cette fonction donne:

\[C(n) = \underbrace{\mathcal{O}(1) + \mathcal{O}(1) + \ldots + \mathcal{O}(1)}_{n \text{ fois}} = \mathcal{O}(n)\]

Deuxième tentative

Une meilleure approche consiste a utiliser la relation mathématique suivante:

\[x^n = \left\{ \begin{array}{ll} 1 & \text{si} & n=1\\[2pt] x^{\frac{n}{2}}\;.\; x^{\frac{n}{2}} & \text{si} & \text{n est pair}\\ x\;.\;x^{\frac{n}{2}}\;.\; x^{\frac{n}{2}} & \text{si} & \text{n est impair}\\ \end{array}\right.\]

Ce qui donne la fonction suivante:

float power( float x, int n)
{
    //base case
    if ( n == 0 )
        return 1;

    // recursive call
    auto val = power(x, n/2);
    return ( n % 2 == 0) ? val * val : x * val * val;

}

La complexité de cette implémentation est \(\mathcal{O}(\log n)\)!!!. Preuve (Check the master theorem)

Greated Common Divisor

Au autre classique absolu est le calcul du plus grand diviseur commun en utilisant la relation Euclide.

Voici un projet pgcd.zip avec des tests unitaires.

La solution de cette fonction est donnee par:

int pgcd(int a, int b)
{
    //base case
    if ( b == 0)
        return a;
    //recursive call
    return pgcd(b, a % b);
}

Memoization

Nous avons explorer dans les sections précédentes tout le puissance et élégance de codage offerte par la récurrence. Cependant, il faut faire attention dans certains cas, ou on réalise des appels redendants.

Afin d’illustrer ce mécanisme, nous allons proposer une solution naïve pour le calcul de nième de terme de la suite de Fibinacci défini comme suit:

\[\text{Fib}(n) = \left\{ \begin{array}{lll} 0 & \text{si} & n = 0 \\[4pt] 1 & \text{si} & n = 1 \\[4pt] \text{Fib}(n-1) + \text{Fib}(n - 2) & & n \geq 2\\ \end{array} \right.\]

La définition naturelle de cette suite invoque une implémentation récursive. Nous allons proposer la solution suivante:

int fib( int n )
{
    //base case 
    if ( n == 0 || n == 1)
        return n;

    //recursive case
    return fib(n - 1) + fib( n - 2);
}

Essayer cette implémentation dans le projet Fibonacci.zip .

Vous allez observer que votre code ne se termine pas dans le dernier test, Cart tout simplement cette implémentation est exponentielle!!

Ceci est du aux duplication de calcul dans cet appel récursif. Pour bien comprendre cette duplication, considerons l’exemple de calculer la valeur \(\text{Fib}(4)\). Le graphiquie suivant montre l’arbre des appels:

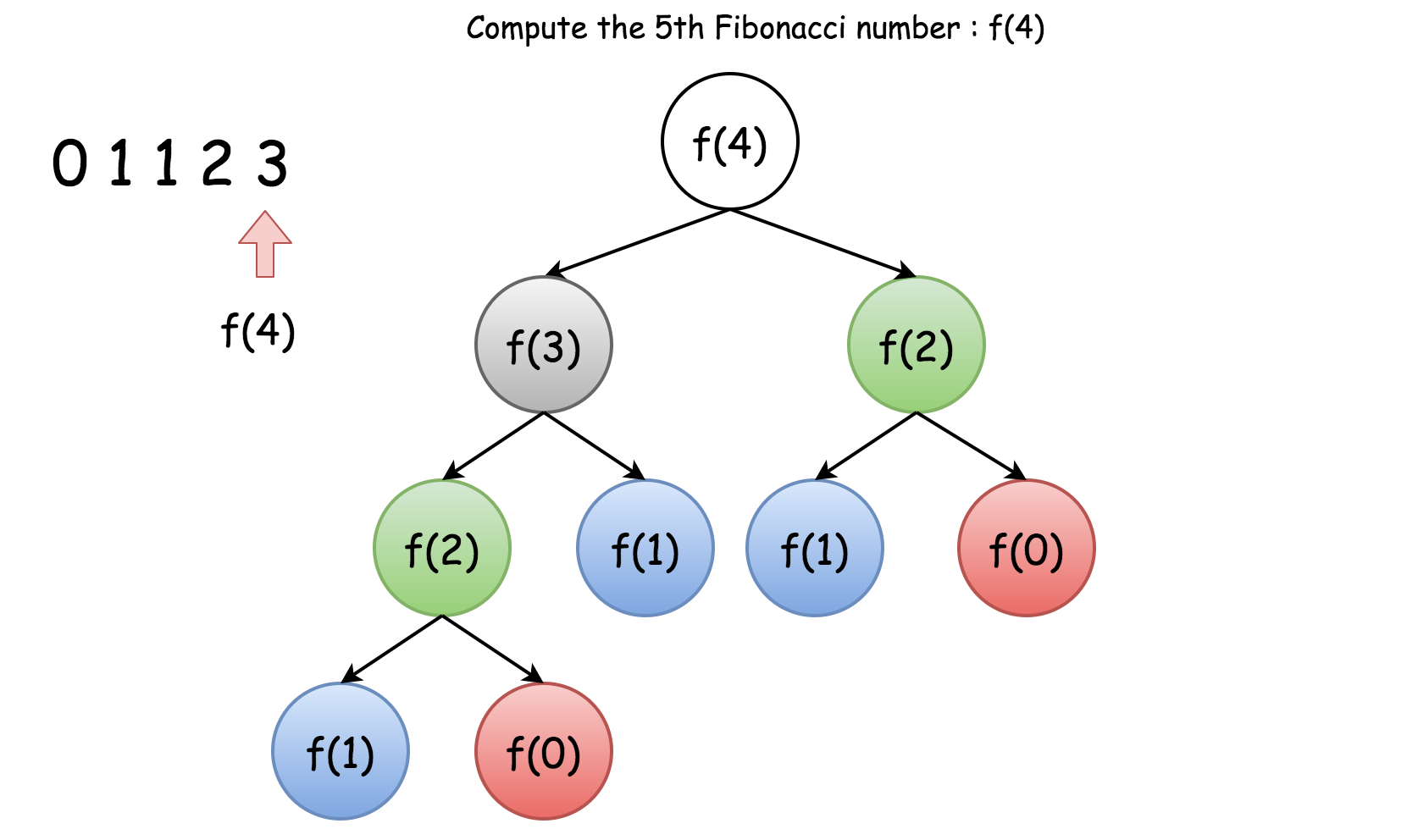
Illustration de l'arbre des appels recursifs pour le calcul de la suite de fibonnaci d'ordre 4.

On voit clairement la repetition des appels. Afin d’eviter ces repetisions, on utilise une techniaue classique de Memoization.

Memoization est une technique d’optimisation de code qui consiste a sauvegarder les valeurs calcules dans un dictionnaire afin d’eviter de recalculer ces valeurs.

Ainsi on va appliquer cette technique dans l’exemple de Fibonnacci afin d’accelerer le calcul et d’obtenir une complexité linéaire \(\mathcal{O}(n)\).

int fib_cache(int n, HashMap & cache)
{
    // Verifiy if we already computed F(n)
    if ( cache.conntainKey(n))
        return cache[n];

    // recurrence
    auto val = fib_cache(n - 1) + fib_cache( n - 2);

    // store the computed value
    cache[n] = val;

    return val;
}

  • Dans ce code, on a utilise une structure avancee HashMap. Son role est de stocker des cles et de vous renvoyer rapidement s’ils existent ainsi que leurs valeurs.

  • Avant de se lancer a calculer la valeur de la fonction \(F\) pour un entier, on verifie tout d’abord, si on l’as pas calcule auparavant.

  • A chaque fois, qu’on calcule une nouvelle valeur, on doit l’ajouter a notre HashMap par : cache[n] = val.

Complexity Analysis

La derniere section de cette lecture introduit un theoreme important pour le calcul de la complexité d’une fonction recursive.

Le Master theorem est un theoreme permet d’obtenir la complexité d’une fonction recursive selon trois parametres (dans sa forme simplifiee).

On note \(T(n)\) le nombre d’operations pour resoudr un problème recursif de taille \(n\). Generalement, on peut ecrire \(T(n)\) selon la forme suivante:

\[T(n) = a\;T\big(\dfrac{n}{b} \big) + \mathcal{O}(n^d)\]

Dans ce cas on possede trois cas:

  1. Si \(d < \log_b a\) alors
\[T(n) = \mathcal{O}\big(n^{\log_ba}\big)\]
  1. Si \(d = \log_b a\) alors
\[T(n) = \mathcal{O}\big(n^d \log n\big)\]
  1. Si \(d > \log_b a\) alors
\[T(n) = \mathcal{O}\big(n^d \big)\]

Afin de comprendre l’application de ce theoreme, appliquons le pour calculer la complexite de la deuxieme verions proposee pour calculer la puissance \(x^n\).

float power( float x, int n)
{
    //base case
    if ( n == 0 )
        return 1;

    // recursive call
    auto val = power(x, n/2);
    return ( n % 2 == 0) ? val * val : x * val * val;

}

Ici dans appel, on reduit la taille du probleme par deux. On obtient la relation de recurrence suivante:

\[T(n) = T\big(\frac{n}{2}\big) + \mathcal{O}(1)\]

Ainsi les valeurs du theoreme sont:

  • \[a = 1\]
  • \[b = 2\]
  • \[d = 0\]

Pour determiner le cas on compare \(d\) et \(\log_b (a)\). On as

\[d = 0\]

et

\[\log_b(a) = \log_2(1) = 0\]

Ainsi, on est dans le deuxime cas. La complexité est donne par

\[T(n) = \mathcal{O}(n^d\log n) = \mathcal{O}(n^0 \log n) = \mathcal{O}(\log n)\]

Tower Hanoi code

Vous pouvez maintenant telecharcher le project Hanoi Towers.zip . Essayer d’implementer vous meme la fonction qui realise les deplacement en suivant l’approche recursive suivante:

Configuration Initiale
Deplacer les n-1 disques en la tige temporaire
Deplacer le plus grand disque dans sa position finale
Deplacer le plus grand disque dans sa position finale