Quick Sort
Quick Sort
Le tri rapide Quick sort est un algorithme de tri formule par Tony Hoare
qui possède une complexité amortie \(\mathcal{O}(n\log\;n)\). Dans le pire
cas il peut avoir une complexité quadratique \(\mathcal{O}(n^2)\). Tous les
langages l’utilisent comme tri de référence.
Ce tri suit aussi l’approche diviser pour regner qui commence par
segmenter le tableau autour d’un pivot choisi par parmi les valeurs du
tableaux. La segmentation consiste a mettre tous les éléments infère rieurs au
pivot gauche et ceux supérieurs a droite. Une fois terminer on est sur que le
pivot occupe sa place dans le tableau trié et il suffit juste de trier les
deux parties ( droite et gauche).

Partition Function
On peut réaliser facilement cette opération si on possède un nouveau tableau.
Cependant il existe méthode très simples pour réaliser cette partition
in-place ( sans avoir a utiliser un autre tableau).
Votre défi consiste a développer cette fonction puis l’utiliser pour implémenter le tri rapide.
Pour ce faire on va utiliser la notation suivante:
pest l’adresse du premier élément dans le tableau.rest l’adresse du dernier élément du tableau qui constitue notre pivot.iest un pointeur qui vérifie que tous les éléments a sa gauche sont inférieurs au pivot.jest pointeur qui vérifie que tous les éléments a sa gauche sont supérieurs au pivot.- Les éléments entre
jetrsont a traités.
Le schéma de cette partition est illustrée dans la figure suivante.
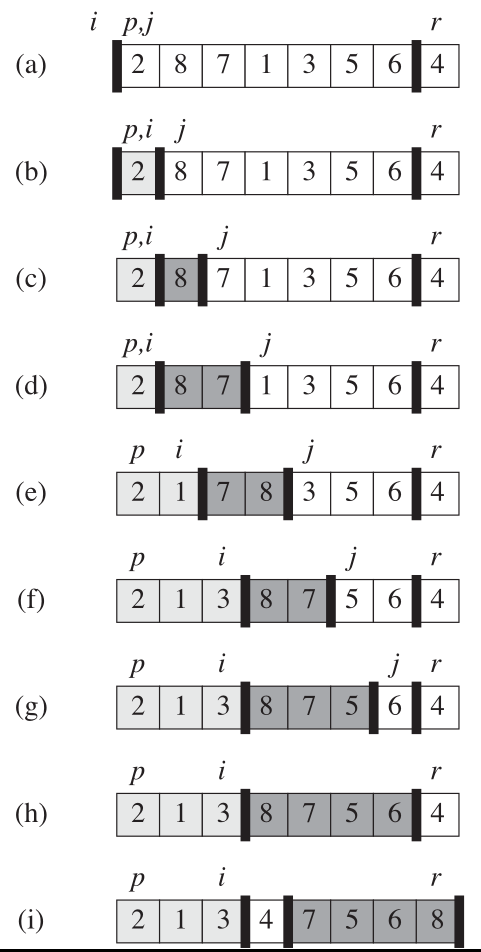
Dans le projet quickSort.zip, vous trouverez le code de départ qui contient des tests pour ce tri. Votre première tache consiste a implémenter la fonction
int partition( int *begin, int * end)
Où
beginest un pointeur sur la première adresse du tableau.endest un pointeur sur la dernier adresse du tableau.- La fonction doit renvoyer la position finale du pivot.
quick sort
Maintenant que vous disposez d’une fonction de partition opérationnelle,
implémenter une fonction récursive quicksort selon le premier schéma.
La fonction possède le prototype suivant:
void quickSort( int *begin, int *end)
Ou
beginest un pointeur sur le premier élément.endest un pointeur sur le dernier élément.
Vous devez maintenant passer tous les tests de ce code.
Sorting by bits
Étant donne un vecteur d’entiers arr. Votre tache est de le trier en ordre
croissant des nombres de 1 dans leurs codage binaire. Dans le cas ou deux
nombres possédant le même nombre de \(1\), on les trie selon leurs valeurs.
Exemple 1:
Input: arr = [0,1,2,3,4,5,6,7,8]
Output: [0,1,2,4,8,3,5,6,7]
Explication: [0] est le seul nombre avec 0 bits.
[1,2,4,8] possèdent 1 bit.
[3,5,6] possèdent 2 bits.
[7] possède 3 bits.
Le tableau trié est [0,1,2,4,8,3,5,6,7]
Exemple 2:
Input: arr = [1024,512,256,128,64,32,16,8,4,2,1]
Output: [1,2,4,8,16,32,64,128,256,512,1024]
Explication: tous les entiers possèdent 1 bit dans leur representation binaire.
on les trie selon leurs valeurs.
Exemple 3:
Input: arr = [2,3,5,7,11,13,17,19]
Output: [2,3,5,17,7,11,13,19]
Voici le sorting_bits.zip le code de départ qui contient le test.
Vous pouvez déjà essayer ce problème avec vos connaissances actuelles. Une fois vous êtes bloques, vous revenez pour lire la suite:
C++ Sort Function
Afin de trier une collection en c++, on utilise la fonction sort déclaré
dans l’entête algorithm. Cette fonction est un template qui peut
s’appliquer a tous les types. Sa syntaxe est la suivante:
sort( iterator begin, iterator end)
beginest un iteraor ou un pointeur sur la première valeur.endest un iterator sur la dernière case.
Tri : Tableau brute
int n = 6;
int arr[] = { 4, 1, 5, 2, 9, 7};
//trier le tableau avec des pointeurs
sort( arr, arr + n);
Tri : Tableau STL
vector<float> arr{3.2, 4.2 , -4, 5.3, 11};
//tri avec begin et end
sort(arr.begin(), arr.end());
Comparator
Maintenant, on tourne notre attention au problème de spécification de la
relation d’ordre. Pour illustrer ce mécanisme, on va considérer la tache de
trier un tableau de points \(P(x,y)\) représentés comme pair<int,int>.
using Point = pair<int, int>;
//Vecteur de points
vector<Point> arr{ {1, 4}, {3, 2}, {8, -1} , {-2, 5} };
Par defauts, en cpp les pairs sont comparees selon leurs premiers valeurs
P.first. Ainsi si on lance un l’algorithme de tri sur ce vecteur on obtient:
sort(arr.begin(), arr.end());
cout << arr << endl;
// ==> (-2, 5) (1, 4) (3, 2) (8, -1)
Supposons maintenant, qu’on veut inverser le tri. ( trier du plus grand au plus petit). Pour ce faire, on utilise un troisième argument de cette fonction qui spécifie comment comparer les clés.
// Trier par le plus grand elements
sort(arr.begin(), arr.end(), greater<Point>());
cout << arr << endl;
// ===> (8, -1) (3, 2) (1, 4) (-2, 5)
Dans le code précédant, on as utilise la fonction greater<Point>() qui sert
pour comparer deux clés. Cette fonction renvoie true si la premier clé est
inférieure a la deuxième.
Supposons maintenant qu’on veut comparer les points maintenant, selon la
deuxième instance P.second. C++ vous offre la possibilite d’ecrire votre
prope fonction de comparaison.
bool cmp(Type & key1, Type & key2);
Cette fonction doit renvoyer true si la cle key1 est plus petite que
key2.
//fonction pour comparer selon la deuxieme valeur
bool cmp( Point &a, Point &b)
{
return a.second < b.second;
}
//trier avec la ccp
sort(arr.begin(), arr.end(), cmp);
cout << arr << endl;
// ==> (8, -1) (3, 2) (1, 4) (-2, 5)
A ce stade la vous êtes biens équipés pour résoudre l’exercice du tri par bits. Penser a écrire votre propre fonction pour comparer les entiers.