Contents

  1. Introduction
  2. Structure
  3. Add Operation

  4. Delete Operation

  5. LL class design
  6. Two Pointers

Introduction

Dans ce chapitre, nous tournons attention à une autre structure de données appelée Liste chainés Linked Lists. Il s’agit d’une structure linéaire ou chaque élément connait l’adresse de son successeur.

Illustration d'une Lined Lists où chaque élément connait l'adresse (pointe) de son successeur.

Comme illustré dans la figure précédente, la structure d’une liste chainée comporte plusieurs noeuds nodes qui sont liés entre eux par des pointeurs ( ou références) sur l’élément suivant.

Il existe deux types de listes chainées:

  • Singly Linked Lists: Chaque nœud connait seulement l’adresse de son successeur.

  • Doubly linked Lists: Un noeud connait non seulement l’adresse de son successeur mais aussi de son prédécesseur.

L’objectif de ce chapitre est de:

  • Comprendre la structure d’une liste chainée.
  • Implémenter la traversée, l’insertion et la suppression d’un élément.
  • Analyser la complexité de ces opérations.
  • Utiliser la technique des deux pointeurs dans des listes chainés.

Structure

Nous commençons a analyser la structure d’une liste chaines simples (Singly Linked List). On peut remarquer que cette structure contient une sequence de noeuds. Chaque noeud contient:

  • Une valeur
  • Un pointeur (flèche bleu) sur l’élément suivant.

Ainsi on peut developper une structure pour stocker les informations de ce neoud.

// Definition for singly-linked list.
struct SinglyListNode {
    int val;
    SinglyListNode *next;
    //Constructor
    SinglyListNode(int x) : val(x), next(NULL) {}
};

Pour représenter toute la liste, nous allons utiliser le nœud head qui se réfère au premier nœud de la liste.

Un point important a remarquer (compare aux vecteurs), est qu’on vient de perdre l’accès direct aux éléments. Par exemple dans la figure précédente, si on veut accéder a l’élément \(15\) est de traverser toute la liste.

Ainsi pour cette structure, il nous faut une complexite lineaire \(\mathcal{O}(N)\) juste pour accéder a un élément.

Une question qu’on doit se poser est pourqu’oi on utilise une telle structure avec un tel inconvénient. La réponse réside dans les deux opérations de ajout et de suppression.

Add Operation

Nous tournons note attention a l’opération principale d’une liste chainée. On va considérer un nœud prev et on cherche a ajouter une valeur juste après ce nœud.

Toujours, Toujours construire un schéma qu'on vous implémenter une liste chainée.

Ading at a given index

  1. Initialiser un noeud curr avec la valeur a insérer.
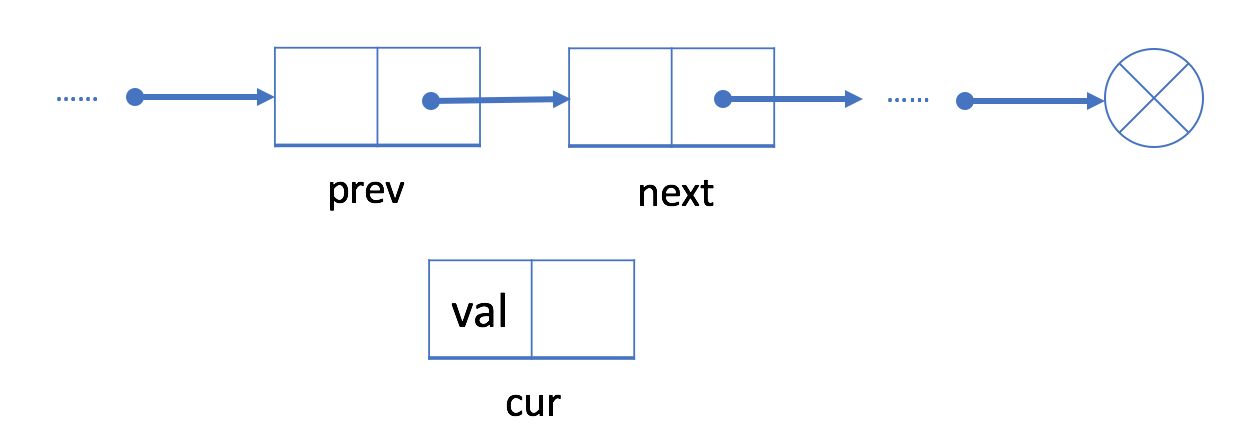
  1. Lier le pointeur de curr au successeur de prev.
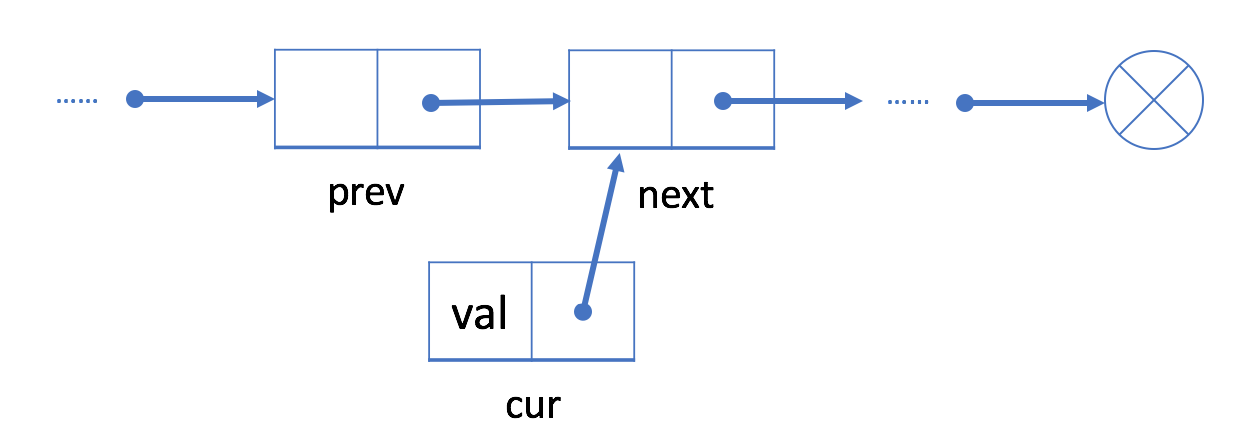
  1. Lier le pointeur de prev au noeud curr.

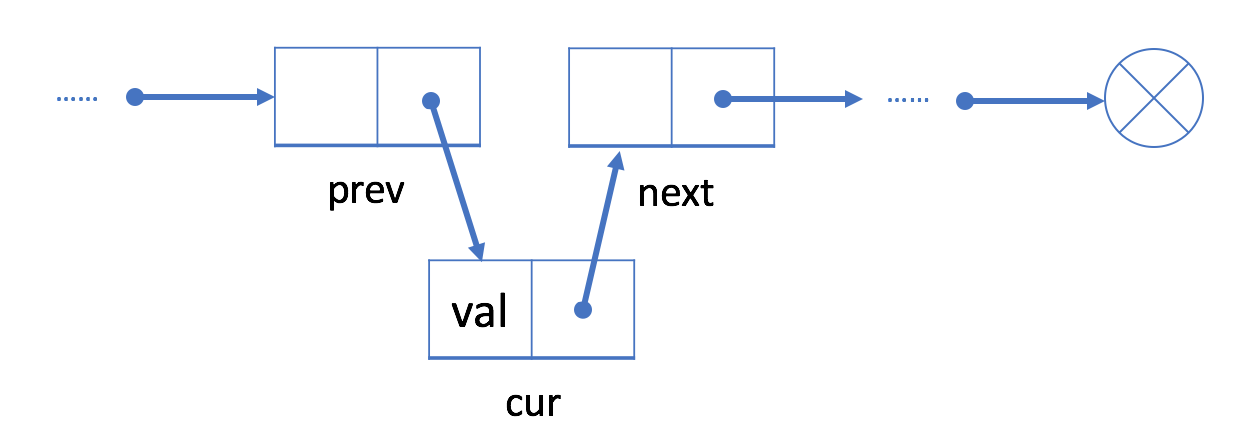
Comme illustré dans le schéma, on peut réaliser cette opération dans un temps constant \(\mathcal{O}(1)\) sans soucier de la capacité (dans les tableaux). Ceci consiste un avantage majeur par rapport aux vecteurs.

Exemple:

Considerons la liste chainée suivante:

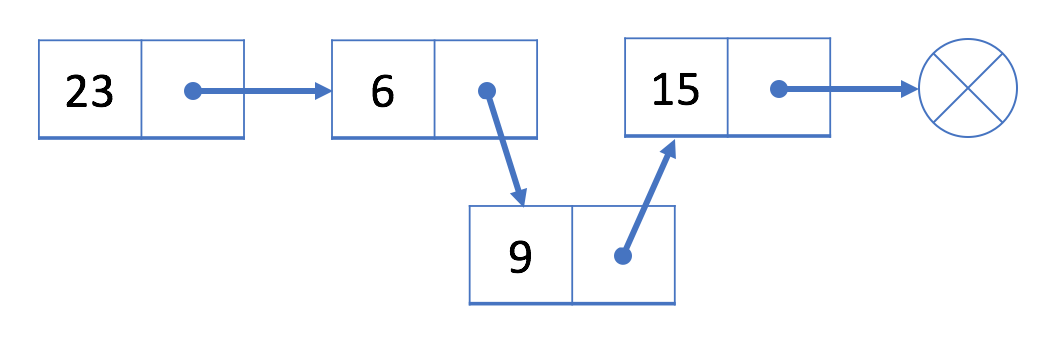
Nous allons insérer la valeur \(9\) après \(6\).

Il faut alors construire un noeud avec la valeur \(9\), Lier le \(9\) a \(15\). Puis il faut lier le noeud \(6\) au noeud \(9\).

Adding at the Beginning

L’algorithme d’insertion change si on considère l’ajout au début de la chaine. Puisque on doit maintenir la référence head sur le début de la liste chainée. Ainsi pour ajouter un noeud au début on doit:

  1. Initialiser le noeud curr.
  2. Lier le noeud curr a head.
  3. Mettre a jour head.

Pour illustrer ce principe, ajouter le noeud \(9\) a notre liste:

  1. Créer un noeud curr avec la valeur \(9\) et le lier a \(23\).
  1. Mettre a jour head au neoud \(9\).

Une question qui se pose est la possibilité d’utiliser la même technique pour insérer un noeud a la fin.

Delete Operation

Similaire a l’ajout, on peut supprimer un noeud curr de la liste chainée, en deux opérations.

  1. Trouver le predecesseur de curr.
  1. Lier le noeud prev et next.

Si on analyse la complexité de cette operation.

  1. On connait déjà la référence next du noeud curr.
  2. Cependant pour accéder a prev, il faut parcourir la liste pour trouver de noeud.

Ainsi la complexité, de cette opération sera linéaire \(\mathcal{O}(N)\) pour une liste simple.

Exemple:

Soit la liste:

  • On cherche a supprimer le noeud \(6\).
  • Traverser la liste pour trouver le predecesseur de \(6\) qui est \(23\).
  • Lier \(23\) (prev) a \(15\) (next).

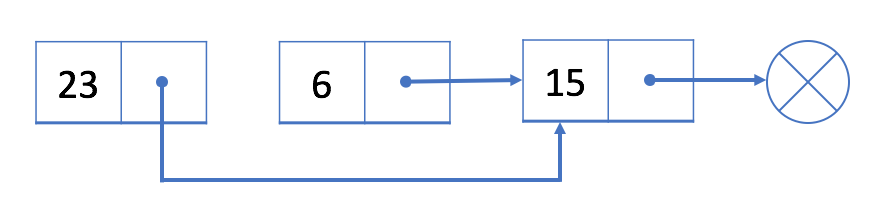
Similaire a l’insertion, la suppression doit être adaptée pour la suppression du premier élément.

Pour supprimer le premier noeud head, il suffit de le déplacer,

  1. Considerson la suppression du premier noeud
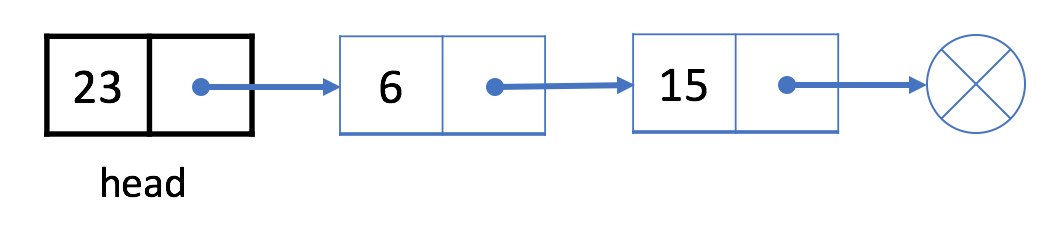
  1. Maintenant \(6\) devient head maintenant:

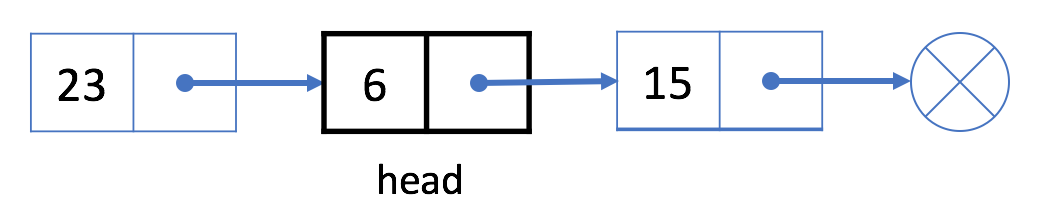
Réfléchir a la question de suppression du élément.

LL class design

Il est temps d’implémenter la classe Linked List avec les operations qu’on as présenter.

Dans le singly_linked_list.zip, vous devez compléter la classe LinkedList avec les membres suivants:

  • LinkedList : initialise la liste chainée.
  • size() : renvoie le nombre d’éléments dans la liste.
  • int get(int index): renvoie la valeur dans l’indice \(i\). Si l’indice est invalide, renvoyer \(-1\).
  • void addAtHead(int val) ajouter le noeud au début de la liste.
  • void addAtTail(int val): ajouter la valeur val a la fin de la liste.
  • void addAtIndex(int index, int val): ajouter la valeur val a l’indice index.
  • void deleteAtIndex(int index) : supprime le noeud dans la position index.
  • operator<< : afficher la liste chainée.

Two pointers

Detect cycle

Cette partie est réservée pour une technique des deux pointeurs déjà introduite dans le chapitre des vecteurs. Afin d’illustrer son avantage dans les listes, essayons de résoudre un classique qui est celui de la détection des cycles dans une liste chainée.

Etant donne une liste, déterminer si elle contient un cycle.

Par exemple la liste chainée suivante contient un cycle \(\left(2, 0 , -4\right)\).

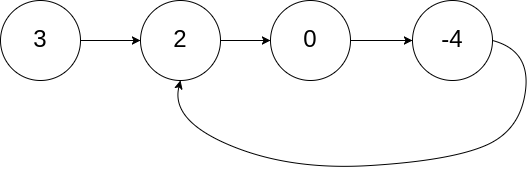
Voici un autre exemple avec deux noeuds.

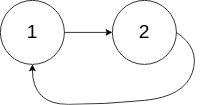
On peut résoudre ce problème en utilisant un HashMap qui stocke les adresses des noeuds déjà visites.

Avec la technique des deux pointeurs, on peut achever cet exercice sans un espace mémoire additionnel pour stocker ces adresses.

Imaginons qu’on possède deux pointeurs qui se déplace dans note liste chainée. On va supposer qu’un pointeur faster est plus rapide dans slower.

  1. Si la liste ne contient pas de cycle, ca serait comme avoir deux coureurs dans une ligne droite. Dans ce cas, faster va arriver a la ligne d’arrive (nullptr) avant son adversaire.

  2. Imaginons maintenant, la même situation mais que la liste chaine contient un cycle. Dans ce cas faster va surmenât attraper son adversaire slower.

Une question classique qui se pose dans ce cas est que doit être la vitesse dans deux pointeurs pour résoudre ce problème.

La stratégie de référence est de déplacer slower toujours par un seul pas. Pour faster, on le déplace par deux pas.

Dans le projet detect_cycles.zip , completer la fonction

bool has_cycle(SinglyLinkedNode *head)

qui reçoit un pointeur sur le head d’une liste chainée et renvoie un booléen indiquant l’existence d’un cycle dans cette liste.