1. Introduction
  2. Règles de calcul
  3. Ordre de grandeur
  4. Etude classique: Recherche

Introduction

L’objectif principal de cette lecture est d’évaluer la complexité d’un algorithme. Il s’agit de mesurer le nombre d'opérations, ainsi que l’espace mémoire, nécessaire pour son exécution. Ceci va nous permettre de déterminer l’évolution du temps d’exécution de ce dernier quand la taille du problème augmente considérablement.

Aussi, cela nous permet de choisir ou de comparer deux ou plusieurs algorithmes puisqu’on va toujours adopter une préférences pour les algorithmes les plus rapides et les moins couteux en utilisation de mémoire.

Somme à deux

Afin d’illustrer cette notion de complexité et comparaison entre deux algorithmes, on va considérer le problème de SommeDeux. Il s’agit d’un problème classique où on reçoit une Tableau L d’entiers et un entier(target) T. Le but est de déterminer l’existence de deux entiers:

\[(a, b) \in L^2,\;\; a + b =T\]

Par exemple, si on considère le tableau \(L = [1, 4, 6]\) alors la fonction renvoie True pour la valeur \(T=10\) car \(6+4 = 10\). Cependant, elle renvoie False pour la valeur \(T=11\) car on peut pas trouver deux valeurs dont la somme est \(11\).

Dans un premier temps on propose l’algorithme simple suivant:

bool brute_force(vecI &nums, int target)
{
    for(int i=0; i<nums.size()-1; i++)
    {
        for(int j=i+1; j<nums.size(); j++)
            if( nums[i] + nums[j] == target)
                return true;
    }

    return false;
}

Cet algorithme applique la notion de recherche brute. i.e pour chaque valeur \(L[i]\), il va chercher dans le reste du tableau pour voir s’il peut trouver une valeur \(L[j]\) tel que \(L[i] + L[j] = T\).

Maintenant on considère une autre approche qui utilise une structure de donnée (mystère pour l’instant).

bool set_search(vecI & nums, int target)
{
    //Same program but using set search
    set<int> cache(nums.begin(), nums.end());

    for(auto v: nums)
        if( cache.find( target - v) != cache.end() )
            return true;

    return false;
}

Ce code mystère utilise une cache pour stocker les valeurs du vecteurs, puis il sert comme une base de donnée indiquant si un élément \(v\) existe ou non dans cette base.

Si on vous donne la possibilité de choisir l’un de ces deux algorithmes, quel choix à prendre?

Pour répondre à cette question on doit considérer les questions suivantes:

  • Pour les deux algorithmes, quel est le temps nécessaire pour obtenir la réponse?

  • Aussi, quel est l’espace mémoire occupé par chaque algorithme?

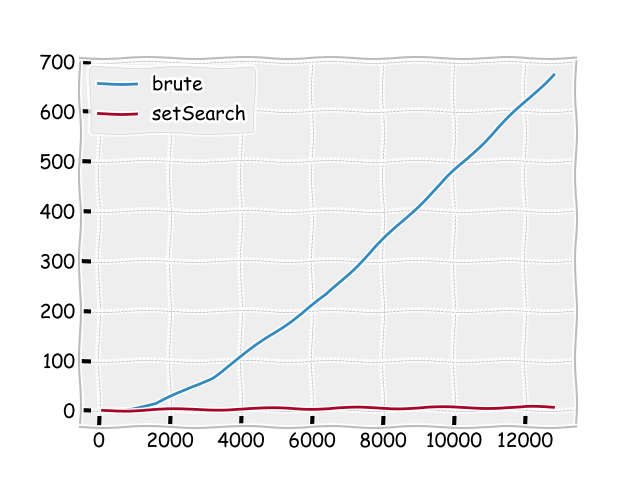
Une première approche est de comparer leurs temps d’exécution pour différente taille Size et de prendre le plus rapide.

Une simulation est effectuée donne le résultat suivant:

Résultats de la simulation qui mesure le temps d'exécution pour les deux algorithmes pour différentes tailles.

  • le temps de la deuxième version est considérablement inférieur que la première!!

  • Chaque fois qu’on double la taille, le temps de la deuxième version double aussi.

Ces résultats montre la supériorité de la deuxième version, cependant on veut caractériser la grandeur de chaque algorithme.

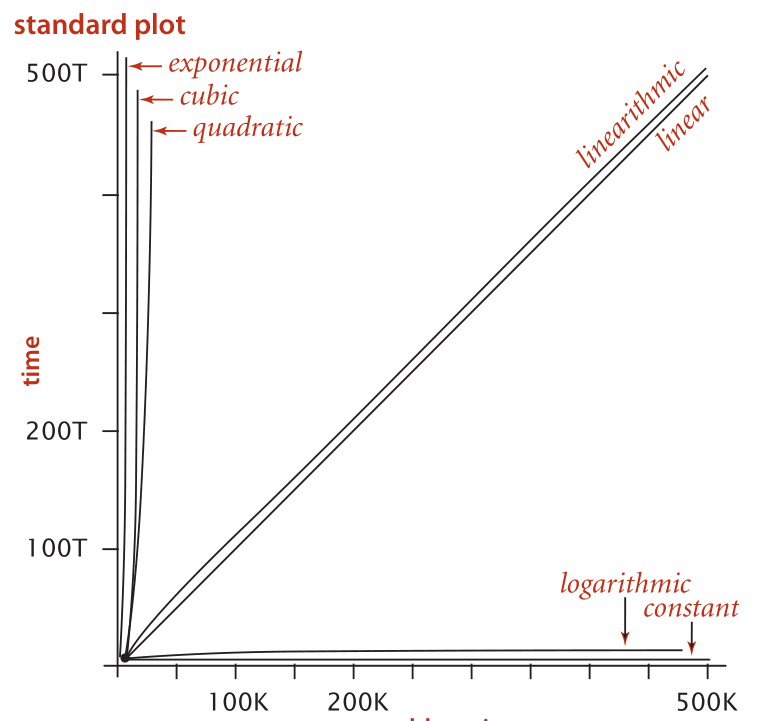
On peut représenter graphiquement la courbe \(N \longrightarrow T(N)\) ou N représente la taille de problème et \(T(N)\) est le temps d’exécution pour un certain algorithme.

Comparaison d'ordre de croissance entre les deux versions.

Deux problèmes avec cette courbe:

  1. La droite de la deuxième courbe représente une constante, alors que c’est pas le cas, juste l’échelle de la première courbe qui l’as rend négligeable.

  2. A partir cette courbe, peut on connaitre l’ordre de celle ci: s’agit il de: \(N\), \(N^2\),\(N^3\) ou \(e^N\).

Une meilleure représentation de cette courbe, consiste à passer dans l’echelle logarithmique. Où on représente \(\log(N) \longrightarrow \log(T(N))\).

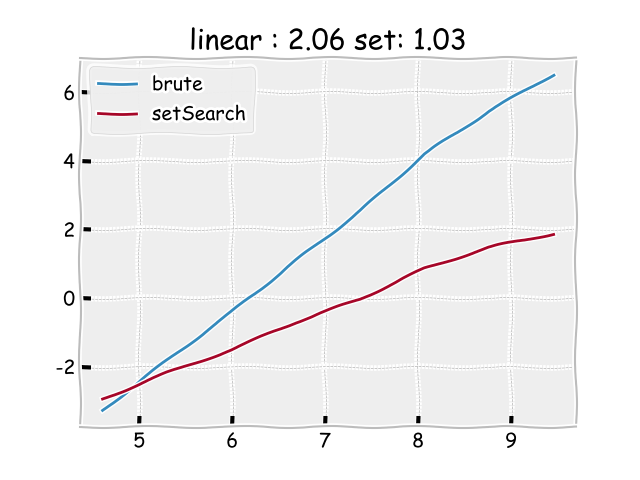
Comparaison d'ordre de croissance entre les deux versions dans l'échelle logarithmique. Dans ce cas les deux fonctions sont des droites et on peut extraire leur ordre comme coefficient directeur de cette droite.

La les deux courbes sont devenues des droites (explication après) et on peut extraire facilement leurs ordre comme étant le coefficient directeur de ces droites. La figure montre que:

  1. La première pente est de \(2.06\), c’est à dire que \(T(N)\) agit comme \(N^2\).
  2. La deuxième pente est de \(1.03\). i.e \(T(N)\) est comparable à \(N\).

Pivot d’un tableau

Pour renforcer cette notion de comparaison, nous allons répéter la même analyse pour le problème des travaux pratiques Pivot Index.

Le problème est pour un tableau T, trouver s’il accepte un indice pivot. Un indice pivot est celui qui vérifie que la somme à a stricte gauche est égale à celle à stricte droite.

Ainsi dans une première version, on étudie un proposition de l’un de vos camarades:

bool brute_force(vecI &nums, int target)
{
    //Solving the pivot problem
    for(int i=0;i<nums.size(); i++)
    {
        auto left = 0;      //left sum
        auto right = 0;     // right sum

        //Calcul somme Gauche
        for(int j = 0; j<i; j++)
            left += nums[i];

        //Calcul somme droite
        for(int j=i+1; j<nums.size(); j++)
            right += nums[i];

        if( left == right)
            return i;
    }

    return false;
}

On le compare à la version suivante:

bool smart_search(vecI & nums, int target)
{
    //Same program but using set search
    auto right = 0;
    for(int i= 0; i<nums.size(); i++)
        right += nums[i];

    auto left = 0; 

    for(int i=0; i<nums.size(); i++)
    {
        right -= nums[i];

        if(left == right)
            return i;

        left += nums[i];
    }

    return false;
}

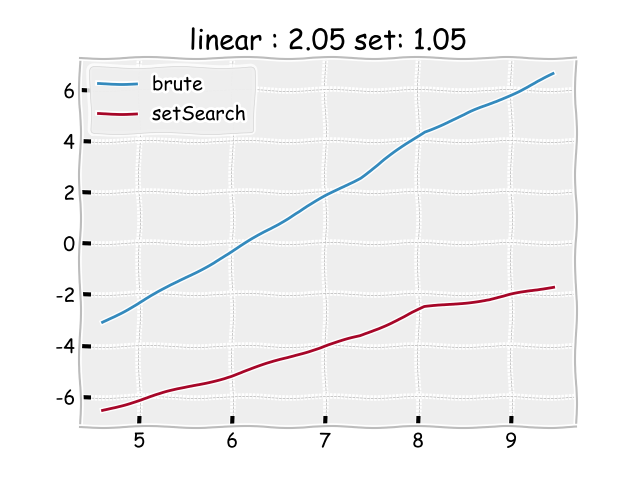
Voici le résultat de comparaison entre ces deux versions:

Résultat de comparaison entre les deux solutions de pivot.

Règles de calcul

Pour déterminer la complexité algorithmique, il est nécessaire de préciser l’architecture utilisée. Pour notre cours, on considère le cas simple d’une machine à processeur unique où on exécute les instructions seront exécutées l’une après l’autre d’une manière séquentielle.

Opérations de base

Aussi on doit définir la notion d’instruction élémentaire, surtout qu’on utilise un langage de haut niveau comme Python qui offre des fonctions avancés en des simples fonctions. A ce titre on mentionne la fonction string.find, on ne peut pas considérer qu’il s’agit d’une opération basique car on sait qu’elle doit chercher dans un tableau pour donner la réponse.

Ainsi on va limiter les opérations de bases au tableau suivant:

  1. Opérations arithmétiques: +, -, *, \, %.
  2. Opérations logiques: <, >, <=, >=, !=, ==.
  3. Opérations de contrôle: Branchement if.

On doit mentionner que ces opérations sont constantes pour les types de base. Par exemple on peut supposer que la comparaison entre deux caractères est constante. Cependant, pour comparer entre deux string c’est pas le cas. Car une égalité entre les chaines implique une égalité entre tous les caractères de la chaine. Ceci invoque alors plus qu’une seule comparaison.

Maintenant qu’on as fixé la notion d’opération de base, on peut analyser le coût réalisé par les deux algorithmes dans le cas de pivot index.

  1. for(int i=0; i<nums.size(); i++: 1 d’initialisation + N répétition.
  2. auto left = 0: 2 opérations.
  3. auto right = 0: 2 opérations.
  4. for(int j=0; j<i; j++) left += nums[j]: Répétition de i Opération.
  5. for(int j=i+1; j<nums.size(); j++) left += nums[j]: Répétition de N-i-1 Opération.
  6. if (left == right) return i: 2 opérations.

Ainsi si on note \(T(n)\) le nombre d’opérations pour accomplir le premier algorithme, on obtient:

\[T(n) = N\left( 2 + 2 + i + N-i-1 + 2\right)\] \[T(n) = N^2 + 5N\]

Ce résultat confirme les résultats trouvé expérimentalement qui indique que T(n) est un polynôme d’ordre 2.

Répétons maintenant le même calcul pour la deuxième version:

  • auto right=0: 2 opérations.
  • for(int i=0; i<nums.size(); i++) right+=nums[i]: \(2N\) opérations.
  • auto left = 0: 2 opérations.
  • for(int i=0; i<nums.size(); i++): Répétition de $N$ opérations:
  • right -= nums[i]: 1 seule opération.
  • if (left == right) return i: 2 opérations.
  • left += nums[i]: 1 seule opération.

Ainsi si on compte T(n) on obtient:

\[T(n) = 2 + 2N + N\left(1 + 2 + 1\right)\]

ce qui donne que:

\[T(n) = 6N + 2\]

Simplification

  • Dans l’analyse de la complexité, est ce que nous avons besoin de réaliser une analyse aussi méticuleuse qui nous donne exactement le nombre d’opérations ou juste l’ordre de croissance de \(T(n)\).

  • On doit apprendre à simplifier et ne considérer que les termes importants

    • Par exemple, pour le premier algorithme on \(T(n) = N^2 + 5N\). Hors on sait que le terme dominant de cette expression est \(N^2\).
    • Aussi, pour le deuxième algorithme on as \(T(n)= 6n + 2\) qu’on va simplifier à \(T(n)=6n\).

  • Ainsi on dit que \(T(n)\) est proportionnel à \(N^2\) dans le premier exemple et proportionnel à \(N\) dans le deuxième.

Notation Big Oh

Cette simplification est bien connue en mathématique sous le nom de Grand O ou dans l’ordre de.

Selon Wikipedia la comparaison asymptotique consiste à étudier la vitesse de croissance d’un fonction au voisinage d’un point ou à l’infini.

En terme mathématiques:

Si on considère deux fonction \(f\) et \(g\) de \(\mathbb{N}\) à \(\mathbb{R}\) qui représentent le temps d’exécution de deux algorithmes. On dit que \(f(n)\) est \(\mathcal{O}(g(n))\) si il existe une constante \(c>0\) et un entier \(n_0\) tel que

\[\forall n \geq n_0 \quad f(n) \leq c g(n)\]
Illustration de deux fonctions f et g qui ont le même ordre de croissance.

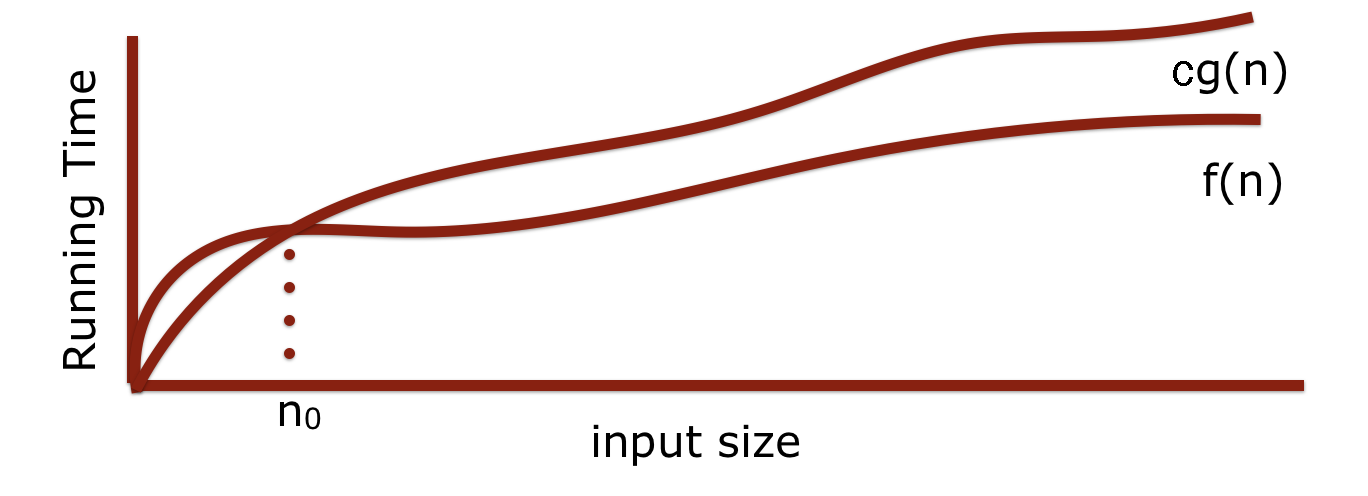
Ainsi avec cette écriture on pourra nous concentrer que sur les termes dominant en ignorant les constantes.

Par exemple:

  • \[2n^3 -2n^2 -4 = \mathcal{O}(n^3)\]
  • \[4n -2 = \mathcal{O}(n)\]
  • \[4 = \mathcal{O}(1)\]

Exercice:

Quel est l’ordre de croissance des fonction suivantes:

  • \[20n^3 + 10\log\; n + 5\]
  • \(2000 \log\; n + 7n\log\;n + 5\).

Notation Bih Theta

Puisque on essaie de majorer \(T(n)\), on dit que l’analyse Grand O est une analyse du pire cas. C’est pas la seule, on peut aussi analyser pour meilleur cas \(\Omega\).

\begin{equation} f(n) = \Omega(g(n)) \quad \Longleftrightarrow \exists M\;\; |\;\; f(n) \geq M g(n) \end{equation}

Une troisième notation est celle du cas en moyenne \(\mathbf{\Theta}\). qui exprime qui exprime une espérance de la complexité d’un algorithme.

\begin{equation} f(n) = \Theta(g(n)) \quad \Longleftrightarrow \exists A,B\;\; |\;\; A\;g(n) \leq f(n) \leq B g(n) \end{equation}

Ordre de grandeur

Catégories

Dans l’analyse de complexité, vous allez rencontrer un ensemble de classes classiques qui sont résumés dans tableau suivant:

  • \(\mathcal{O}(1)\): Constant.
  • \(\mathcal{O}(n)\): Linéaire.
  • \(\mathcal{O}(n\log\; n)\): Quasi linéaire.
  • \(\mathcal{O}(n^2)\): Quadratique.
  • \(\mathcal{O}(n^3)\): Cubique.
  • \(\mathcal{O}(n^k)\): Polynomiale.
  • \(\mathcal{O}(k^n)\; k>1\): Exponentielle.

Exemples

  • Constant

Ces algorithmes qui ne dépendent pas de la taille du problème. Ils sont super efficace.

- Exemple classique est la suppression de la fin d'un tableau.
- Exemple du future!!
- Ajouter ou  supprimer  d'une pile.
- Ajoute ou supprimer d'une file.
  • Linéaire:

La majorité des boucles for (simple non pas imbriquées) sont linéaire.

for(int i=0; i<nums.size(); i++)
    nums[i] = 0;

Ce code est proportionnel à la taille du tableau, ainsi \(\mathcal{O}(N)\).

Les algorithmes linéaires sont aussi préférés car leur temps évolue de la manière que la taille du problème.

  • Quadratique

A chaque fois qu’on imbrique deux boucles qui dépendent de la taille, on obtient un algorithme quadratique.

for(int i=0; i<nums.size(); i++)
{
    for(int j=0; j<nums.size(); j++)
    retulst ++;
}

Avec cette boucle on obtient \(\mathcal{O}(n^2)\). Ce taux de croissance est très lourd (On cherche à l’éviter).

Instructions cachées

Dans l’analyse de votre code, il faut faire attention aux instructions cachée derrière une fonction ou une classe.

A titre d’exemple, reprenons l’exemple de recherche par ensemble du premier problème:

bool set_search(vecI & nums, int target)
{
    //Same program but using set search
    set<int> cache(nums.begin(), nums.end());

    for(auto v: nums)
        if( cache.find( target - v) != cache.end() )
            return true;

    return false;
}

Si on cherche à analyser ce code on doit répondre à deux questions:

  • set<int> cache(numbs.begin(), nums.end()): Quel est le nombre d’opérations?
  • for(auto v: nums): Répétitions \(N\) fois.
  • if cache.find(target - v) != cache.end()): Quel est le nombre d’opérations?

Pour la première instruction, il s’agit de construire un set d’entier, si on cherche dans la documentation Set, on trouve que ce constructeur de complexité linéaire \(\mathcal{O}(n)\).

Pour la deuxième opération, qui applique la méthode find qui à une complexité logarithmique \(\mathcal{O}(\log\;n)\).

Ainsi si on combine ces informations on trouve que la complexité est:

\[T(n) = n + n(\log\; n) = \mathcal{O}(n\log\;n)\]

Exercice:

Evaluer la complexité du code suivant:

vector<int> arr;

for(int i=0; i<n; i++)
    arr.insert(0, i+1);

Recherche

Un problème classique dans la tableaux est celui de la recherche dans un tableau trié. On ne l’as gardé à ce chapitre pour pouvoir apprécier la différence entre deux algorithme classiques qui sont:

  • Recherche linéaire
  • Recherche dichotomique

Dans ce problème, on considère qu’on possède un tableau \(L\) qui est trié et qui contient \(n\) éléments. Le but est déterminer si un élément \(s\) existe dans le tableau.

Recherche Linéaire

Il s’agit de l’algorithme classique déja traité dans le cours et qui ne prend pas considération la propriété que l’algorithme est trié.

for(int i=0; i<nums.size(); i++)
    if( nums[i] == s)
        return s;

Une analyse simple donne que ce code est linéaire \(\mathcal{O}(n)\) qui explique bien la description de la recherche.

Recherche dichotomique

Dans la recherche dichotomique ou binary search, on exploite la propriété du tri du tableau. Dans chaque itération, on divise le tableau sur deux. On compare alors la valeur au milieu (pivot). Si cette valeur correspond à celle qu’on cherche on as terminé. Sinon le fait que le tableau est trié nous permet de réduire à la taille de recherche à deux puisque on termine soit dans la partie à gauche soit dans la partie à droite.

Cette recherche est illustrée dans la figure suivante:

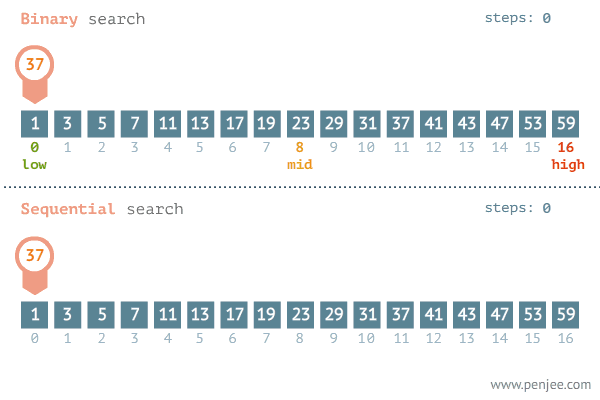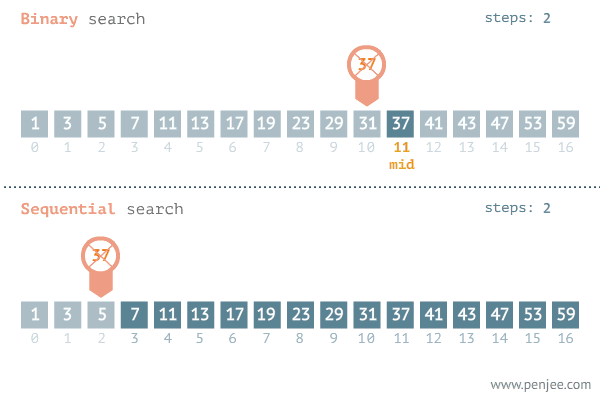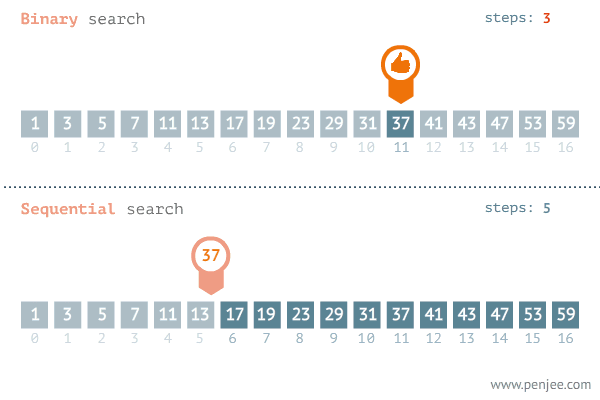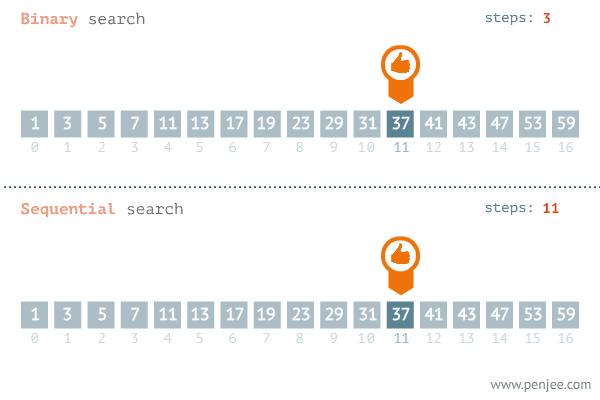
Pour cet exemple, il nous faut une étude mathématique, On peut remarquer que dans chaque opération on réalise des deux opérations élémentaires qui sont la \emph{division} pour calculer le milieu et la comparaison pour voir où est ce qu’on va chercher dans la suite. La taille du problème est réduite à la la moitié dans chaque opération. On peut écrire alors la formule de \(f(n)\) par:

\[\begin{equation} f(n) = \underbrace{2}_{\scriptsize\text{taille n}} + \underbrace{2}_{\scriptsize \text{ taille} \frac{n}{2^1}} + \underbrace{2}_{\scriptsize \text{ taille} \frac{n}{2^2}}+\ldots + \underbrace{2}_{\scriptsize \text{ taille} \frac{n}{2^k}} = 2 (k+1) = \mathcal{O}(k) \end{equation}\]

Il nous reste maintenant à déterminer la valeur de \(k\). On sait que

\[\begin{eqnarray} \frac{n}{2^k} &\leq & 1 \\ \log_2(n) - k & \leq & 0\\ k & \geq & log_2(n) + 1 \end{eqnarray}\]

Ainsi on vient de prouver que la complexité de la recherche dichotomique est \(\mathcal{O}(log{n})\) qui est une complexité logarithmique. Ce qui offre une grande amélioration comparé a celle de la recherche linéaire. Dans la séance pratique on va comparer le temps d’exécution des deux algorithmes pour confirmer cette réduction.