Working with pointers
Liste d’exercice.
Grasping
V1V2P1P2
Dans l’exercice v1v2p1p2, on vous demande d’éxécuter le programme suivant et de donner leur résultat.
int v1 = 10;
int v2 = 25;
int *p1 = &v1;
int *p2 = &v2;
*p1 += *p2;
p2 = p1;
*p2 = *p1 + *p2;
cout<< v1 << " " << v2 << endl;
cout<< *p1 <<" " << *p2 << endl;
parameterMystery1
Dans l’exercice ParameterMystery1, on vous demande de produire le résultat du programme suivant:
int parameterMystery1(int a, int &b, int* c)
{
b++;
a += *c;
cout<< b << " "<< *c<< " " << a << " " << c << endl;
c = &a;
return a-b;
}
int main()
{
int a = 4;
int b = 8;
int c = -3;
int d;
d = parameterMystery1(a, b, &c);
parameterMystery1(c, d, &b);
parameterMystery1(b, a, &d);
cout<< a <<" " << b << " " << c <<" " <<d << endl;
}
Pour unifier le résultat, on suppose que les les variables sont stockées dans les mémoires suivantes:
- a est stockée dans
0xaa00 - b est stockée dans
0xbb00 - c est stockée dans
0xcc00 - d est stockée dans
0xdd00
parameterMystery2X
Similaire à l’exércice précédant, dans ParamterMyster2, on vous demande de produire le résultat du programme suivant:
string * parameterMyster2X(string & s1, string s2)
{
s1 += "1";
s2 += "2";
cout<< s2 << " -- " << s1 <<endl;
s1 += "!!!";
return &s1;
}
int main()
{
string s1 = "hi";
string s2 = "bye";
string s3 = "yo";
string * s4 = new string(s3);
string* s5 = nullptr;
parameterMyster2X(s1, s3);
s5 = parameterMyster2X(*s4, s2);
parameterMyster2X(s2, *s5);
cout<<s1<<" "<<s2<<" "<<s3<<endl;
cout<<s4<< " " << *s4 << " " << s5 << *s5 << endl;
}
Les espaces mémoires des variables est le suivant:
- s1 est dans
0x1100 - s2 est dans
0x2200 - s3 est dans
0x3300 - s4 est dans
0x4400 - s5 est dans
0x5500
Arrays using pointers
Il est temps d’utiliser vos connaissances en Tableau et pointeur pour
résoudre des problèmes un peu plus difficile. Dans la suite on vous fournit un
projet cmake qui contient un fichier pour chaque exercice. Le projet
nécessite la bibliothèque google test.
En cas où vous n’arrivez pas à l’exécuter, enlever lest fonctions test, et
remplacez les par vos propre tests.
Vous devez télécharer le code de départ qui est dans Pointer_homework.zip
Pivot Index
Etant donné un tableau d’entiers nums, calculer son indice pivot.
L’indice pivot d’un tableau est où la somme des éléments à sa stricte gauche est égale à la somme de ceux qui sont à la stricte droite.
- Si l’indice est \(0\), alors la somme à gauche est considérée nulle.
- De même, pour l’indice à la fin, la somme a droite est nulle.
Ecriver une fonction qui possède le prototype suivant:
int pivotIndex( vector<int> & nums)
{
}
La fonction doit renvoyer le premier indice pivot. En cas où on ne trouve aucun indice, on revoit la valeur \(-1\).
Exemple 1
Input: nums = [1,7,3,6,5,6]
Output: 3
Explication:
La valeur du pivot est 3.
Somme gauche = nums[0] + nums[1] + nums[2] = 1 + 7 + 3 = 11
Somme droite = nums[4] + nums[5] = 5 + 6 = 11
Exemple 2
Input: nums = [1,2,3]
Output: -1
Explication:
Il n y'as aucun indice qui vérifie cette condition
Exemple 3
Input: nums = [2,1,-1]
Output: 0
Explication
L'indice pivot est 0.
Somme gauche = 0 (Pas d'élément à gauche de 0)
Somme droite = nums[1] + nums[2] = 1 + -1 = 0
Le fichier avec les tests est dans array_pivot.cpp.
Largest Number
Etant donné un vecteur des entiers nums, Trouver le plus grand élément dans ce
tableau.
Votre tache est de confirmer si c’est élément est au moins plus grand que le double du reste. Si c’est le cas vous renvoyer son indice, sinon vous renvoyer -1.
Le vrai défi, est de réaliser ce exercice avec des pointeurs avec juste une seule passe du tableau.
Exemple1
Input: nums = [3, 6, 1, 0]
Output: 1
Explication: 6 est le plus grand eniter, et pour chaque valeur dans le tableau
x, 6 est supérieur ou égal au double de x
Exemple 2
Input: nums = [1, 2, 3, 4]
Output: -1
Explication: 4 est inférieur au double de 3.
Vous trouverez le code de départ dans largest_number.cpp.
Plus One
Etant donné un tableau stl non vide qui représente les chiffres d’un
entier positive \(n\). Votre tache est de renvoyer une tableau stl qui
contient les chiffres de \(n+1\).
Le prototype de la fonction est le suivant:
vector<int> plusOne(vector<int> & nums)
{
}
Exemple 1:
Input: digits = [1,2,3]
Output: [1,2,4]
Exemple 2:
Input: digits = [4,3,2,1]
Output: [4,3,2,2]
Exemple 3:
Input: digits = [0]
Output: [1]
Vous trouvez le code de départ dans add_one.cpp.
Matrices
Pascal Matrix
Ecrire une fonction generate(int numRows) qui reçoit un nombre de lignes
numRows et renvoie une représentation du Triangle de Pascale.
Dans ce triangle, chaque élément est calculé en se basant les la ligne précédente comme ceci:
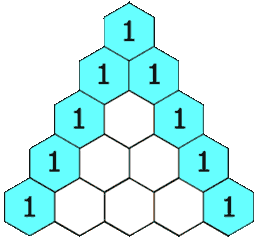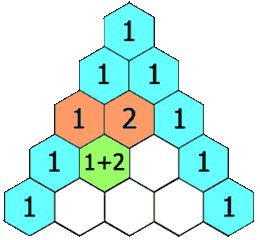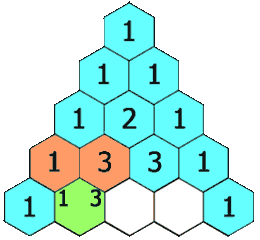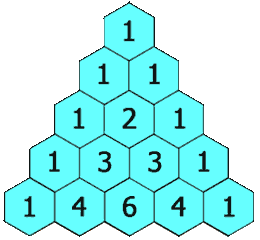
Vous avez le chois soit de réprésenter ce triangle en utilisant des vecteur stl soit d’utiliser les tableaux avec la gestion de la mémoire.
Exemple 1
Input: numRows = 5
Output: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]
Exemple 2:
Input: numRows = 3
Output: [[1],[1,1],[1,2,1]]
Vous trouvere le code avec les tests dans pascal_matrix.cpp.
Spiral
Etant donné une matrice m x n, on cherche à écrire une fonction qui renvoie
tous ces éléments dans un ordre spiral.
vector<int> spiralOrder(vector<vector<int>> & M)
Exemple 1

Input: matrix = [[1,2,3],[4,5,6],[7,8,9]]
Output: [1,2,3,6,9,8,7,4,5]
Exemple 2

Input: matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
Output: [1,2,3,4,8,12,11,10,9,5,6,7]